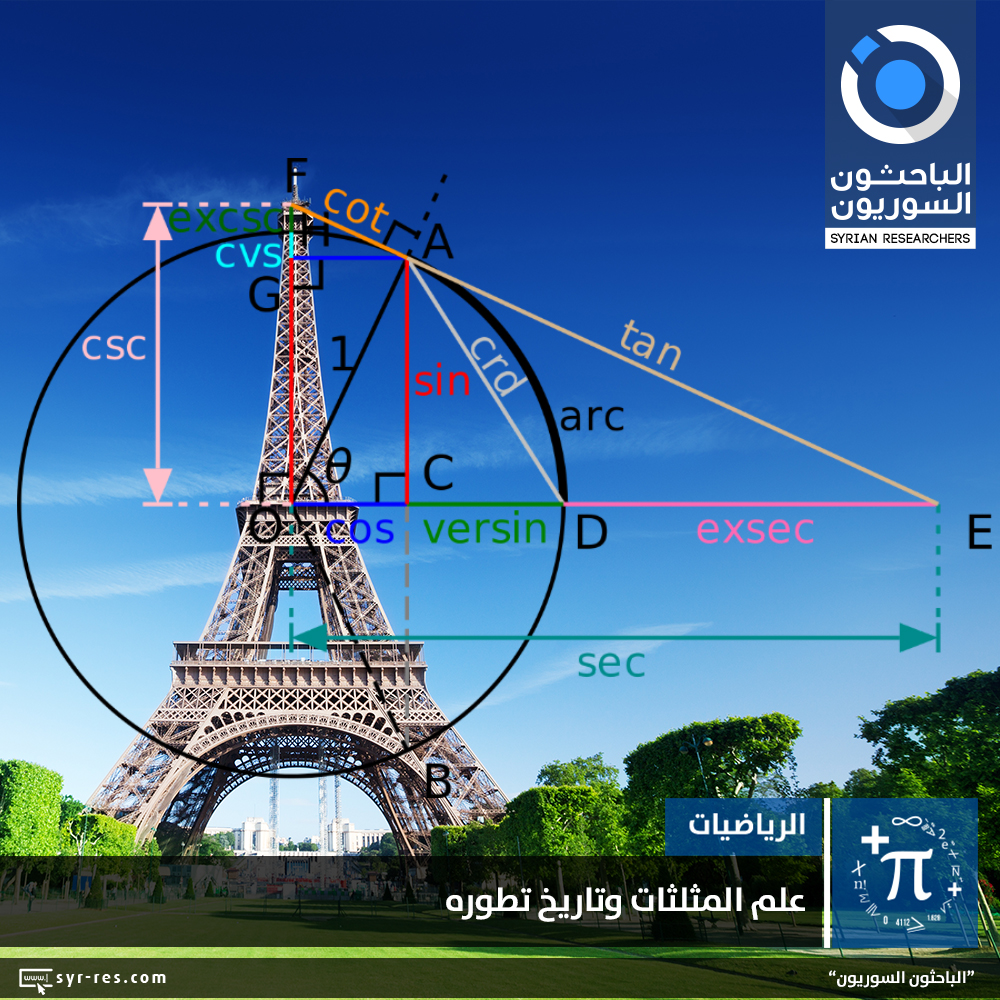
علم المثلثات وتاريخ تطوره
الرياضيات >>>> الرياضيات
لعلم المثلثات صلاتٌ بفروع أخرى رياضياتية كالتحليل العقدي (المركب) و اللوغاريتمات و حساب التفاضل والتكامل.
يعود اشتقاق كلمة Trigonometry (المثلثات بالانكليزية) إلى القرن السادس عشر حيث تمثل نحتاً من جذرين من اللغة الإغريقية ( Trigōnon ) وتعني مثلث triangle و ( Metron ) وتعني قياس measure.
رغم الأدلة على استخدام البابليين لعلم المثلثات، و نبوغ الفراعنة فيه، إلا أن الأدلة المعروفة لعلم المثلثات الحالي تعود ربما لبدايات القرن الثالث قبل الميلاد، حيث بدأت بأعمال بعض الرياضيين الإغريق كإقليدس وتالس و فيثاغورث، كما أن بعضاً من أكثر المساهمات أهمية (مثل دالة الجيب sine) أتت من الهند في القرن الخامس الميلادي، حيث برع الهنود بعلم المثلثات، وليس معروفاً فيما إذا كانوا قد طوروا علم المثلثات بمعزل عن سابقيهم الإغريق أو بتأثير من كتاباتهم. ويرى فيكتور كاتز Victor Katz في كتابه "تاريخ الرياضيات (الطبعة الثالثة)" (Pearson، 2008)، أن علم المثلثات قد تطور على يد العلماء الإغريق و اليونان حسب حاجات عصرهم.
مدخل من خلال أمثلة عملية :
المثال الأول: معرفة ارتفاع مبنى من خلال معرفة طول ظله
يمثل هذا المثال الحالة العلمية الأولى التي دعت القدماء لاكتشاف مفهوم الظل، ربما الكلمة العربية (الظل) المستخدمة للدلالة على tangent تدل بشكل او بآخر على ذلك.
باستخدام عصا صغيرة معلومة الطول، يمكن معرفة نسبة طولها إلى طول ظلها في، هذه النسبة تعرف الميل و يمكن استخدامها لمعرفة ارتفاع المبنى بمجرد معرفة طول ظله ضربه بتلك النسبة، بطريقة مشابهة يمكننا الاستدلال على طول سارية مركب شراعي بمجرد معرفة الميل عند نقطة ما من سطح المركب بمجرد معرفة بعد تلك النقطة عن قاعدة السارية، و زاوية النظر والتي تمثل الميل.
Image: https://www.syr-res.com/
إن قيمة الميل تختلف باختلاف الدرجة، ذلك المفهوم الذي طوره القدماء كجزء من 360 جزءاً من دائرة كاملة، في محاولة لإيجاد وحدة لقياس الزوايا، ففي مثالنا كلما ابتعدنا عن السارية تنقص زاوية النظر لرأس السارية، و مع اقترابنا من قاعدة السارية تزداد، وبالتالي من خلال قياس تلك الزاوية يمكننا معرفة ارتفاع أي سارية، أو مبنى او جبل.
Image: https://www.syr-res.com/
إن تقسيم الدائرة الكاملة الى 360 درجة، تعود أصوله إلى البابليين ربما، من خلال أعمالهم لتطوير التقويم السنوي كما سنرى لاحقاً في هذه المقالة.
المثال الثاني، الجيب وجيب التمام والظل:
اعتماداً على ما هو معروف حول العديد من أطوال أضلاع وزوايا مثلثٍ قائمٍ. توجد نسبيتين مثلثيتين واسعتي الاستخدام وهما: دالة الجيب "sine function" وتكتب بالشكل sin(x)، ودالة جيب التمام "cosine function" وتكتب بالشكل cos(x).
كما هو معروف في المثلث القائم، لكل زاوية ضلع مقابل، و مجاورين يشكلا معا تلك الزاوية، واعتماداً على أطوال تلك الأضلاع يمكن معرفة كل النسب المثلثية للزاوية المعنية.
في المثلث القائم، يسمى الضلع المقابل للزاوية القائمة بالوتر hypotenuse. أما الضلعين المتبقيين فيسميان بالساقين. وعادة ما نكون مهتمين (كما في المثال أعلاه) بزاوية أخرى غير الزاوية القائمة. وما كنا قد دعوناه بـ "الارتفاع" في المثال أعلاه يأخذ على أنّه طول الساق المقابل opposite للزاوية المطلوبة. وبالمثل فإنّ الميل يأخذ على أنّه طول الساق المجاور adjacent. وعند التطبيق على قياس زاوية، فإنّ الدوال المثلثية الثلاث تنتج تركيبات متنوعة من النسب لأطوال أضلاع المثلث.
بعبارة أخرى فإنّ:
ظل الزاوية A = طول الضلع المقابل مقسوماً على طول الضلع المجاور.
جيب الزاوية A = طول الضلع المقابل مقسوماً على طول الوتر.
جيب تمام الزاوية A = طول الضلع المجاور مقسوماً على طول الوتر.
من مثالنا عن سارية المركب الشراعي سابقاً، فإنّ العلاقة بين الزاوية وظلها يمكن أن تحدد من خلال رسمها البياني، كما هو موضح أدناه. الرسوم البيانية للجيب وجيب التمام مضمنة كذلك في الرسم البياني.
Image: https://www.syr-res.com/
جدير بالذكر، أنّ كل من هذه الدوال مرتبط بعضها ببعض من خلال مجموعة كبيرة ومتنوعة من المعادلات المعقدة تعرف باسم المتطابقات، والتي هي عبارة عن معادلات صحيحة على الدوام بغض النظر عن قيمة المتغير.
كل دالة مثلثية تملك أيضاً معكوساً يمكن استخدامه لإيجاد زاوية من خلال نسبة الأضلاع. معكوس sin(x) و cos(x) و tan(x) هو arcsin(x) و arccos(x) و arctan(x) على الترتيب.
Image: https://www.syr-res.com/
بطبيعة الحال علم المثلثات يشمل دراسة كل أنواع المثلثات و ليس فقط القائمة منها، و تعرف عملية معرفة أضلاع المثلث و زاوياه بحل المثلث، و كما تشمل أيضا دراسة المثلثات الكروية وهي التي تكون أضلاعها معرَّفة بشكل أقواس على سطح كرة.
بشكل عام و لأجل أي مثلث إقليدي ومن خلال معرفة عدد معين من الأضلاع و الزوايا، يمكن الاستدلال على البقية بالاستفادة من مجموعة من العلاقات العامة التي تربط الأضلاع و الزاوايا، سنستعرض أهمها فيما يلي :
* قانون الجيب، وينص على أنّه إذا عرفت قيمة واحدة من النسب الثلاث زاوية\ضلع، فيمكن تحديد بقية القيم من خلال معرفة واحدة منها:
sin(A)/a = sin(B)/b = sin(C)/c
* قانون جيب التمام، وينص على أنّه يمكن إيجاد ضلع مجهول من خلال معرفة ضلعين والزاوية المحصورة بينهما. وهو في الأساس نظرية فيثاغورث مع معامل تصحيح بالنسبة للزوايا غير القائمة:
c^2 = a^2 + b^2 – 2ab.cos(C)
* حقيقة أنّ مجموع زوايا أي مثلث يساوي 180°.
A + B + C = 180°
تاريخ علم المثلثات:
سلكت المثلثات طريقًا مماثلًا للجبر: فلقد طورت في الشرق الأوسط القديم ومن خلال التجارة والهجرة انتقلت إلى اليونان والهند وبلاد العرب وأخيراً أوروبا (حيث صيغت النسخة الأخيرة التي من خلالها يتم تعليم معظم الناس في يومنا هذا).
الخط الزمني للاكتشافات المثلثية معقد بعض الشيء وذلك ينبع من حقيقة أنّ الهند والجزيرة العربية استمرتا في التفوق دراسيًا لعدة قرون بعد مرور المعرفة عبر الحدود الثقافية. فعلى سبيل المثال إنّ اكتشاف مادافا Madhava للسلسلة اللانهائية للجيب في العام 1400م كان غير معروف لأوربا حتى قام اسحاق نيوتن باكتشافه بشكل مستقل في العام 1670م.
إن إسهامات علماء الحضارة الإسلامية باختلاف أعراقهم و مشاربهم، في علم المثلثات، كانت ثورية لدرجة أن أغلب العلاقات المثلثية التي تستخدم في الصفوف الأخيرة من المرحلة الثانوية في سوريا مثلاً هي من ابتكارهم و تطويرهم.
كما يعود الفضل للبتاني و هو عالم عربي من الجزيرة السورية، و يعرف في الغرب باسم (Albategnius) في اكتشاف و تطوير فرع المثلثات الكروية spherical trigonometry ذو الأهمية البالغة في علم الفلك، إذ خدمه في دراسة القبة السماوية بافتراض أن النجوم والكواكب هي نقاط في سطح كرة، رغم خطأ الفرضية الأخيرة فيزيائياً، إلا أنها كانت السبب المباشر لاكتشاف فرع المثلثات الكروية، كما أن لأبي الوفاء البوزجاني العالم الفارسي الذي عاش وعمل في بغداد، إسهامات مهمة في علم المثلثات (للاطلاع على مقالنا السابق عن العالم البوزجاني هنا) ، فمثلاً يعود له الفضل في اكتشاف المتطابقات المثلثية التي تعرف اليوم بصيغتها التالية:
sin(a+b) = sin(a) cos(b) + sin(b) cos(a)
sin(a-b) = sin(a) cos(b) - sin(b) cos(a)
cos(a+b) = -sin(a) sin(b) + cos(b) cos(a)
cos(a-b) = sin(a) sin(b) + cos(b) cos(a)
بالاضافة لمشتقاتها:
sin(a) = 2sin(a)cos(a)
cos(2a)= cos²(a) –sin²(a)
sin²(a)+cos²(a)=1
وكذلك:
2sin(a) cos(b)= sin(a+b)+sin(a+b)
2cos(a) cos(b)= cos(a+b)+cos(a-b)
كما اكتشف بعض القوانين في المثلثات الكروية
Image: https://www.syr-res.com/
اكتشاف علاقة الجيب و التجيب:
وتبعاً لهذه التعقيدات، سنركز بشكل خاص على اكتشاف وعبارة الجيب وجيب التمام والظل.
ابتداءً من بلاد ما بين النهرين، قام البابليون في القرن السابع قبل الميلاد – إبان الامبراطورية البابلية الحديثة- بتحديد تقنية لحساب عدد مرات ظهور النجوم الثابتة على البروج. والتي تستغرق حوالي 10 أيام بالنسبة لنجم ثابت مختلف ليظهر تمامًا قبل الفجر، وهناك ثلاث نجوم ثابتة في كل من الأبراج الفلكية الاثني عشر.
10 × 12 × 3 = 360
والعدد 360 قريب بما يكفي للـ 365.24 يومًا في السنة ولكنها أكثر ملاءمةً للتعامل معها ، و هذا ما جعل البابليين يقسمون السنة الى 360 يوماً ثم يضيفون خمسة أيام لنهاية كل عام.
تقسيمات مطابقة تقريبًا وجدت في نصوص حضارات قديمة، كمصر ووادي السند. فوفقاً لأوتا ميزباخ Uta Merzbach في كتابه "تاريخ الرياضيات" (Wiley، 2011) فإنّ تكييف هذه التقنية البابلية من قبل عالم الفلك والرياضي الإغريقي إبسقلاوس الإسكندري حوالي 150 قبل الميلاد كانت أشبه بمصدر إلهام لهيبارخوس نيقية (190 إلى 120 قبل الميلاد) لبدءِ أسلوب تقسيم الدائرة إلى 360 درجة.
وفقاً لجيرالد تومر Gerald Toomer، قام هيبارخوس باستخدام الهندسة بتحديد قيم مثلثية لدالة سماها بدالة الوتر Crd والتي تتعلق بدالة الجيب بالعلاقة:
Crd(2a)/2 = 3438 sin (a)
وادعى تومر أنّ هيبارخوس عرف دالته الـ Crd عند مجالات قيمتها 7.5 درجة (1/48 من الدائرة).
ولاحقًا قام بطليموس الإسكندري (90 – 168 ميلادية) في كتابه "المجسطي" في العام 148م بتعزيز عمل هيبارخوس من خلال تحديد قيم مثلثية في جدول للزوايا بين 0 و 180 درجة، و بخطوة قدرها نصف درجة، أي أنه بدأ من الصفر ثم 0.5 قم 1 ثم 1.5 وهكذا.
أقدم سجل معروف لدالة الجيب جاء من الهند في القرن الخامس الميلادي في عمل لأريابهاتا Aryabhata (476 إلى 550 ميلادية). الفقرة 1.12 من "الأريابهاتيا Aryabhatiya" (499)، فبدلاً من تمثيل الزوايا بالدرجات، قسم الزاوية القائمة إلى 24 جزءاً، و أوجد قيم الجيب الموافقة لكل منها، وكانت هذه نقطة الانطلاق لكثير من المثلثات في القرون التالية.
الفئة التالية من العلماء الكبار الذين ورثوا علم المثلثات جاءت من العصر الذهبي للحضارة الإسلامية. فقد قام المأمون الخليفة العباسي السابع ومؤسس بيت الحكمة في بغداد (813 - 888 ميلادية)، برعاية ترجمة كتاب بطليموس "المجسطي" وكتاب أريابهاتا الآنف الذكر إلى العربية. وبعد ذلك قام الخوارزمي (780 - 850) بتقديم جداول دقيقة للجيب وجيب التمام في كتابه الجداول الفلكية أو ما يسمى بـ "زيج السند هند" وقد أتمه سنة 820 ميلادية، وقد دخلت كلمة الزيج للعربية حينها بمعنى الجداول الحسابية، ومن خلال ترجمة هذا العمل من العربية إلى اللاتينية، دخلت معارف علم المثلثات إلى أوربا لاحقاً.
يرى جيرالد تومر Gerald Toomer في كتابه "قاموس السيرة العلمية 7"، أن النسخة العربية الأصلية من كتاب "زيج السند هند" قد فُقدت، إلا أن ثمة نسخة مزيدة كتبت من قبل الفلكي الأندلسي مسلمة بن أحمد المجريطي (حوالي العام 1000 للميلاد)، لاحقاً ترجمت نسخة المجريطي إلى اللاتينية في جنوب إنكلترا في حدود عام 1126 ميلادية.
تطبيقات علم المثلثات اليوم :
مثلت جداول الزيج ربما بداية لتكون مفهوم الدالة المثلثية، إذ أنها تربط بين متحولين الأول يأخذ قيمه من الزوايا الممكنة بينما بمثل الثاني القيم الموافقة، إلا أن مفهوم الدوال 'التوابع' المثلثية أَعيد صياغته للتوافق مع المفاهيم الحديثة للرياضيات، و لتتوسع معه مجالات تطبيقاته الممكنة، لتتخطى حدود الهندسة و الفلك، إذ شكلت صيغة أولر الجبيبية مثلا للتابع الأسي
exp(x) = cos(x)+i sin(x)
ومدخلاً لعلم التحليل العقدي بتطبيقاته التي لا حصر لها، ومهدت المجال للرياضي والفيزيائي فوريه لتقديم سلاسله التي عرفت باسمه فيما بعد، إذ أكدت بإمكانية كتابه أي دالة دورية كسلسلة لانهائية من الدوال الجيبية الموزونة بمعاملات مناسبة، وتبع ذلك تقديمه لتحويله، تحويل فوريه، و يعرف كل ذي صلة بالهندسة ما يعنيه الأخير وما حمله من تطبيقات في مجالات شتى، وكما مثلت محاكاة حركة النواس بتغير دالة مثلثية 'الجيب' ثورة في الفيزياء و لا سيما في دراسة أنظمة اهتزازية امتدت لتشمل حركة النابض و التخميد، و حتى نماذج لورنتز لتمثيل العلاقة بين النواة و الإلكترون، و ما تلا ذلك من تطبيقات، شملت كل الأنظمة ذات الطابع الاهتزازي وصولا لميكانيكا الكم في تمثيل الأنظمة الفيزيائية الكمية التي تهتز بين حالتين، وعلى سبيل المثال لا الحصر، تنبأ الفيزيائي البولندي- الأمريكي ازدور رابي باهتزاز الذرة بين حالتين مستثارة و أساسية ( غير مستثارة) بشكل جيبي، بطريقة تكون فيها الذرة أغلب الوقت بحالة تركيب احتمالي بين تلك الحالتين الحديتين، حيث يمكن تمثيلها بشعاع يهتز على سطح كرة ( كرة بلوخ).
Image: https://www.syr-res.com/
وفي علم الاتصالات مثلت التوابع المثلثية، حوامل شبه مثالية لنقل الإشارت لمسافات طويلة عبر مفهوم التعديل التماثلي بالتردد FM أو بالمطال AM أو بالصفحة PM
نعود إلى مثالنا الأول، في معرفة ارتفاع المباني من خلال معرفة ظلها، إذ إن عملية شبيهة تقوم بها كل الطائرات عند التحليق و بالتحديد عند تغيير ارتفاعها.
المصادر:
هنا
هنا
هنا